


Next: Conclusion
Up: Calculation
Previous: The gluonic bag constant
In the standard fashion [32,33] we now estimate the critical
temperature Tc (no baryonic chemical potential 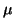 )
of a deconfinement phase transition from the bag constant
3 x nf x Bq. For this we take the value
nf x B=0.007 GeV4
for
)
of a deconfinement phase transition from the bag constant
3 x nf x Bq. For this we take the value
nf x B=0.007 GeV4
for 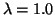 GeV, and with
GeV, and with
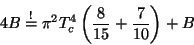 |
(6) |
we obtain
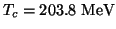 .
From SU(3) Yang-Mills lattice simulations one expects a
smooth decrease of the gluon condensate for temperatures near
260 MeV [34]. Therefore, we would have
to correct the bag radius at zero temperature towards
higher values near the phase transition. For comparison, we determine
the critical temperature from the phenomenological
value
B=4.54 x 10-4 GeV4 of Ref. [9] as Tc=102.8 MeV.
This is too low, since otherwise
the deconfinement phase transition would have already
been seen experimentally [35].
.
From SU(3) Yang-Mills lattice simulations one expects a
smooth decrease of the gluon condensate for temperatures near
260 MeV [34]. Therefore, we would have
to correct the bag radius at zero temperature towards
higher values near the phase transition. For comparison, we determine
the critical temperature from the phenomenological
value
B=4.54 x 10-4 GeV4 of Ref. [9] as Tc=102.8 MeV.
This is too low, since otherwise
the deconfinement phase transition would have already
been seen experimentally [35].
Marc Schumann
2000-10-16