Arithmonic, Arithmetic,Harmonic,

Geometric and Golden Means

All means as particular cases of a more general concept: "The Rational Mean", some examples extracted from the book: : “LA QUINTA OPERACI�N ARITM�TICA, Revoluci�n del N�mero” (Title translation: The Fifth Arithmetical Operation, Number Revolution) ISBN: 980-07-6632-4. Copyright �. All rights reserved under international Copyright Conventions. Author: D. G�mez.

CONTENTS:

• Arithmetic Mean (Ar)
• Harmonic Mean (Hm)
• ARITHMONIC MEAN (ATM)))
• Geometric Mean
• Golden Mean
• Conclusions
• GO  TO &--MAIL  TO:

Arithmetic Mean (Ar)

The arithmetic mean is the rational mean between fractions having equal denominators. As an example, the arithmetic mean between three values 4/3, 5/4, and 6/5 is the rational mean between them by previously making their denominators the same:

Harmonic Mean (Hm)

The harmonic mean is the rational mean between fractions having equal numerators. As an example, the harmonic mean between three values 4/3, 5/4, and 6/5 is the rational mean between them by previously making their numerators the same:

Arithmonic Mean (ATM)

The arithmonic mean ATM_i of order i between n arbitrary values is the rational mean between them by previously making the numerators of the first fraction up to the i-th fraction the same, and the denominators of the i-th fraction up to the last one the same. There are n arithmonic means between n numbers.

As an example given four values 9/8, 2, 2, 2 the following are the successive four arithmonic means of the first, second, third and fourth order (ATM₁, ATM₂ , ATM₃, ATM₄ ):

As an interesting property notice that 9/8* 2* 2* 2= 9 and the product:

This means that in the same way as the initial four values 9/8, 2, 2, 2 define --by defect and excess-- the fourth root of 9, also the four arithmonic means are closer approximations --by defect and excess-- to the same root.

 

Geometric Mean (Gm)

See roots web page.

Golden Mean

The irrational number:

known as the Golden Mean value (a number satisfying the golden proportion: p/q= q/(p+q)) is a solution to the equation x²+x-1=0 and is related to the Fibonacci's sequence: 1, 1, 2, 3, 5, 8, 13,...

Given the following two initial ratios:

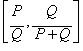
The rational process for approximating the irrational value of the Golden Mean is:

(Note: The acronym "Mr" means Rational Mean, Rm)

Step 1:

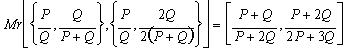
Step 2:

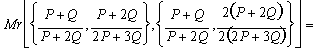
Step 3:

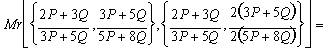
Step 4:

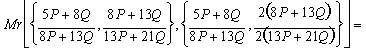
and so on...

at each stage of the process we get two closer rational approximations to the Golden Mean. Notice that the numerical coefficients bring out Fibonnaci's sequence.

Conclusions

Based on the new rational mean concept, it is clear that the traditional credo on "means" should be redefined. It is striking to realize that the above general concept on the rational mean embracing all the means, have been passed over all through the history of Arithmetic, specially when considering that, for example, the Arithmonic Mean is an indispensable arithmetical tool for solving roots by agency of higher order convergence methods.

 

 

[TOP PAGE]

 

Copyright � 1993-2002

All rights reserved under international Copyright Conventions.

No part of this page may be reproduced, stored or transmitted in any form or by any means without the prior permission of the author: D. G�mez.

Last revision: 2002