Scalene and Isosceles Partitions (SIP)

The scalene partition is a new simple construction for dividing ---by means of compass and straightedge--- any line segment AB into n equal parts.

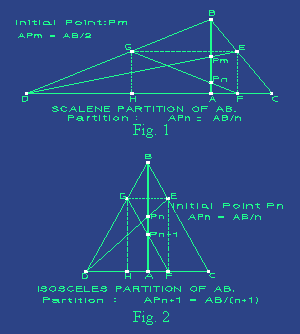
See Fig. 1
Given any line segment AB, trough point A draw a segment line CD perpendicular to AB whose length is (n+1)/2 times the length CA. The length CA is arbitrarily chosen.
Find midpoint Pm of AB.
Draw BC and BD and let the line DPm cut BC at E.
Trough point E draw EF parallel to AB and EG parallel to CD.
The line FG cuts AB at point Pn, then :

APn = AB / n

And the line segment AB can now be divided into n equal segments of length APn.

.The Isosceles Partition

Given any line segment AB, Isosceles partition is a new construction for finding ---by agency of compass and straightedge--- the following sequence of partitions (See Fig. 3).

AB/n, AB/(n+1), AB/(n+2), AB/(n+3), ...

See Fig. 2. Given any line segment AB draw a segment line CD perpendicular to AB whose midpoint is located at point A and its length is CD = 2CA. The length CA is arbitrarily chosen. Given a starting point Pn in AB whose distance from A is :

APn = AB / n

Draw BC and BD and let the line DPn cut BC in E. Trough E draw EF parallel to AB and EG parallel to CD. The line FG cuts AB at point Pn+1, then :

APn+1 = AB / (n+1)

The line segment AB can now be divided into n+1 equal segments.

(See Fig. 3)
By continuously repeating the above steps we will find sequentially the points Pn, Pn+1, Pn+2 ... whose corresponding distances from A are :

AB/n, AB/(n+1), AB/(n+2), AB/(n+3), ...

.The Isosceles-Fibonacci Partition. Published by JTfM, Berlin, 1997.

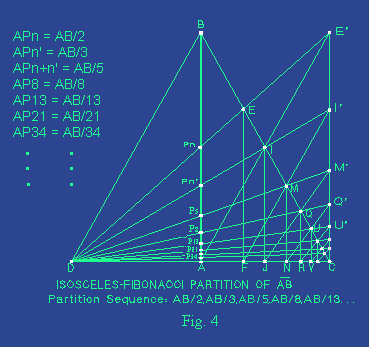
See Fig. 4.
Given any line segment AB, draw a segment line CD perpendicular to AB whose midpoint is located at A and its length is CD=2CA. The length CA is arbitrarily chosen.
Given two starting points Pn and Pn' whose corresponding distances from A are :

APn = AB / n , APn' = AB / n'

Draw the lines BC, BD. Draw the line CE' parallel to AB, so CE' = AB. Let the line DPn cut BC at point E and draw EF parallel to AB. Let the line DPn' cut BC and CE' at points I and I' respectively. The line I'F cuts BC at point M, and the line DM cuts AB at point Pn+n', then :

APn+n' = AB / ( n+n' )

The above expression can be used as a second-order linear homogeneous recurrence relation. Thus, we can repeat the above steps, this time using the starting points Pn' and Pn+n', then by continuously repeating this procedure we can easily construct a sequence of partitions whose denominators belongs to the well known FIBONACCI sequence.

In Fig. 4, I deliberately chose the starting points Pn and Pn' so their distances from A are :

APn = AB / 2 , APn' = AB / 3

That is, n = 2, n' = 3, consequently APn+n' = AP5 = AB / 5. Of course, it is evident that one can start with n = 1 and n' = 2.

.Conclusions

The Scalene Partition

(See Fig. 1) The Scalene construction allows to find any segment of length AB/n without constructing any other previous partitions of AB. For this reason it is very interesting to compare this new Scalene partition with Proposition 9, Book 6 of Euclid's Elements.

In this way, in order to find the partition AB/n of the line segment AB, Scalene partition requires drawing seven (7) initial segments lines while Euclid's partition requires only four (4) lines, however, in order to draw the auxiliary segment line CD the Scalene partition requires only (n+1)/2 additional compass movements while Euclid's Proposition requires n additional compass movements.

Considering that we are exclusively talking about compass and straightedge, this comparison makes much sense when n > 8, in such a case, Scalene Partition requires fewer compass movements than Proposition 9, Book 6 of Euclid's Elements. Actually, this compass-movements comparison should be made considering all the lines involved in the construction. In this way, I hope the reader will be interested in doing so for the following SIP Variation (Fig 1-1) :

Based on this, Scalene Partition becomes more efficient than Proposition 9, Book VI of Euclid's Elements. Actually, I must say tha in Euclid's Proposition 9 we could use only (n+1)/2 additional compass movements for constructing the auxiliary segment line, in such a case both SIP and Euclid constructions are very similar, however, we are asuming Euclid's proposition just as it was stated.

The Isosceles Partition.

In Fig. 3 draw the lines EPn+1, IPn+2, MPn+3. Now, it is easy to prove that the lines EPn+1 and BD are parallels. In the same way, the lines IPn+2 and ED, the lines MPn+3 and ID, . . . and so on, are parallels. Based on this, Isosceles partition (Fig 3) becomes as an extremely simple method which only involves the construction of the aforesaid parallels, that is:

EPn+1 parallel to BD , IPn+2 parallel to ED , MPn+3 parallel to ID , and so on ...

One can see that Isosceles partition yields an unique sequence involving both the even and odd partitions :

AB/3 , AB/4 , AB/5 , AB/6 , ... , AB/(n-1) , AB/n

Moreover, the most important fact is that Isosceles Partition offers much more than the above sequence. It is a general method which also permits ---with so much simplicity--- the generation of many partition sequences, including FIBONACCI (Fig 4), even-odd-denominator sequences and other higher order sequences.

[TOP PAGE]

No part of this page may be reproduced, stored or transmitted in any form or by any means

without the prior permission of the author: D. G�mez.

Last revision: 2002