��������������������������������������������������������������

 

�   � � �   �   �

Media Racional

Algunas definiciones y observaciones de la Media Racional (Mediant generalizada) extra�das del libro: �LA QUINTA OPERACI�N ARITM�TICA, Revoluci�n del N�mero� ISBN: 980-07-6632-4. Copyright �. Todos los derechos reservados. Autor: D. G�mez.

 

CONTENIDO:

• Media Racional. Definici�n
• Ejemplo
• Operaci�n Racional General. Definici�n:
• Comentarios

 

La Media Racional

(Mediant Generalizada)

Media Racional. Definici�n.

Dado un conjunto V de n n�meros racionales positivos ordenados de acuerdo a sus magnitudes:

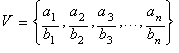
La expresi�n:

es un valor medio (Media Racional, Rm) entre los valores extremos  (a₁/b₁), (a_n/b_n) del conjunto V:

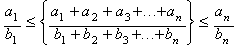
Una notaci�n general para m�ltiples medias racionales puede ser expresada as�:

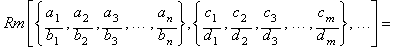
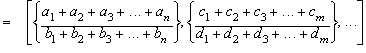
Ejemplo:

El siguiente caso:

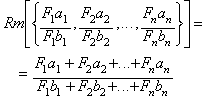
es tambi�n la media racional entre los mismos n n�meros racionales, modificando esta vez la forma de cada fracci�n mediante los factores: F₁, F₂,..., F_n.

Podemos decir que dado cualquier conjunto de n valores escogidos a voluntad (enteros, racionales o irracionales) ordenados en orden creciente:

y dado otro conjunto [F₁, F₂, F₃, . . ., F_n] de valores positivos cualesquiera (enteros, racionales or irracionales), entonces la expressi�n:

es la Media Racional entre los valores v₁,v_2,v₃, ... ,v_n

Operaci�n General Racional (Gro). Definici�n:

Podemos ir m�s lejos a�n y definir la Operaci�n General Racional (Gro) (no necesariamente un valor medio dentro del conjunto dado inicialmente) entre n valores arbitrarios v₁,v_2,v₃, ... ,v_n como lo haremos a continuaci�n:
Dados n valores v₁=a₁, v₂=(-a₂/b₂), v₃=(a₃/b₃), v₄=-a_4, . . . , v₅=-a_n , la Gro entre esos valores viene dada as�:

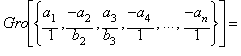
M�s a�n, dadas n funciones racionales: f₁(x)/g₁(x), f₂(x)/g₂(x), f₃(x)/g₃(x), ..., f_n(x)/g_n(x), la Operaci�n General Racional (no necesariamente un valor medio entre los valores de esas funciones) es:

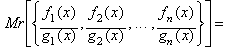
En algunos casos la Gro ser� la Media Racional entre esas n funciones racionales.

Cualquier algoritmo basado en la Media Racional ser� llamado en adelante: Proceso Racional.

Es necesario decir que el an�lisis de la Media Racional (Rm) ha sido restringido �a lo largo de toda la historia de las matem�ticas� al caso espec�fico de la operaci�n llamada Mediant (n=2) y algunas curiosas propiedades de las series de  Farey, los c�rculos de Ford, el �rbol de Stern-Brocot  y la generaci�n de los convergentes en las fracciones continuas simples, ejemplo:

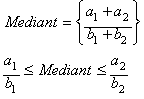
Comentarios

Algunos matem�ticos usualmente establecen que est� operaci�n no est� bien definida dentro del conjunto de los n�meros racionales, esto es, que la media racional trabaja exclusivamente con pares ordenados de enteros en lugar de n�meros racionales. Como ejemplo, calculemos la media racional:

Rm[3/2, 4/3]= 7/5

y calculemos la media racional entre esos mismos n�meros pero cambiando 3/2 por su forma 6/4:

Rm[6/4, 4/3]= 10/7

Se han utilizado los mismos valores, la misma operaci�n y sin embargo el resultado es diferente.

Ahora, si debido a esto nosotros argumentamos que esta operaci�n no est� "bien definida" dentro del conjunto de los racionales, entonces deber�amos decir tambi�n que las siguientes operaciones matem�ticas no est�n bien definidas dentro del conjunto de los n�meros racionales, principalmente porque la Media Racional es el principio fundamental que las regula:

�La Media Arm�nica: Es la Media Racional entre fracciones con numeradores iguales.

�La Media Aritm�tica: Es la Media Racional entre fracciones con denominadores iguales.

�La Media Aritm�nica: Es la Media Racional entre fracciones donde un grupo de denominadores y numeradores son iguales de acuerdo a una regla espec�fica.

�Media Geom�trica

�Generaci�n de los convergentes de las fracciones continuas generalizadas

�N�meros transcendentales y algebraicos

�M�todos de Bernoulli, Newton y Halley para la resoluci�n de ecuaciones algebraicas

�Expansiones en series de potencias (series de Maclaurin-Taylor).

�Definici�n de las operaciones aritm�ticas de los n�meros irracionales

�Estad�sticas

�Centro de gravedad

�C�rculos de Ford

�Fracciones de Farey

Contrariamente a la corriente actual de pensamiento de los matem�ticos modernos, est� claro que todo ese concepto sobre la "buena" o "mala" definici�n de esta operaci�n dentro del conjunto de los racionales deber�a ser considerado desde un punto de vista totalmente distinto, puesto que esa visi�n restrictiva  est� basada en una concepci�n exclusivamente cartesiana de los n�meros y esa no tiene porque ser necesariamente la herramienta ideal para comprender sin distorsiones de ning�n tipo la verdadera esencia de la Cantidad y sus diversas manifestaciones.

As�, contrariamente a los fundamentos absolutistas del sistema Cartesiano, el N�mero no deber�a ser considerado simplemente como un "Valor Absoluto" (exclusivo valor decimal) sino como una entidad con valor absoluto y valor relativo. De la misma manera que las flores nos brindan m�ltiples propiedades naturales: belleza, color, aroma, etc. tambi�n el N�mero nos brinda mucho m�s que un simple "valor absoluto", �ste sostiene adem�s un valor relativo (La forma de la fracci�n) y su localizaci�n espec�fica dentro del esquema general de los n�meros. La importancia de todas esas propiedades ser�n evidentes al lector cuando estudie la nueva operaci�n: Media Aritm�nica. Un punto muy importante, corolario de todos las nuevas propiedades y m�todos que tienen su base en la simple aritm�tica de la Media Racional, es el hecho cierto que el sistema Cartesiano ha servido muy especialmente a la despersonalizaci�n del N�mero confin�ndolo al triste papel de no ser m�s que un simple valor absoluto (valor decimal).

En verdad es realmente inquietante  comprender que los m�s antiguos matem�ticos (Babilonios, Griegos, etc.) ciertamente ten�an al alcance de sus manos la herramienta aritm�tica m�s simple y elemental  (La Media Racional) para lograr desarrollar todos esos llamados "algoritmos avanzados" que han sido consagrados como los m�s resaltantes logros sacados a luz gracias exclusivamente al sistema cartesiano y la creaci�n de los decimales. Basados en todas las evidencias hist�ricas, al parecer la extremadamente simple operaci�n aritm�tica Media Racional desarrollada brevemente en estas p�ginas y con m�s detalle� en el libro �La Quinta Operaci�n Aritm�tica� no tiene precedentes en toda la larga historia de la resoluci�n de ecuaciones.

De todos los nuevos y elementales procesos aritm�ticos mostrados en el libro "la quinta operaci�n aritm�tica" el lector podr� comprender las siguientes importantes consideraciones:

�El sistema cartesiano no puede ser considerado como un sistema fundamental de la filosof�a natural sino como una creaci�n artificial que aparte de ser extr�nseca a las propiedades naturales de los n�meros, principalmente contribuye a distorsionar y viciar la imagen genuina de la Cantidad relegando al N�mero al simple papel de un valor absoluto.

�Las operaciones aritm�ticas de los n�meros irracionales pueden ser definidas de manera muy sencilla mediante el Proceso Racional y basados en el N�mero en s� mismo en lugar de utilizar las creaciones y opiniones personales de Dedekind y Cantor.

�Las tradicionales fracciones continuas no son m�s que un caso particular (Fracciones continuas de segundo orden) de una concepci�n general llamada: �Fracciones cont�nuas generalizadas� (Fracciones fractales), las cuales producen representaciones peri�dicas de los n�meros algebraicos de cualquier grado. Cualquier representaci�n de los n�meros irracionales de grado superior al segundo se obtiene totalmente distorsionada cuando se utilizan las tradicionales fracciones continuas �Fracciones continuas de segundo orden�.

�Sorprendentemente no hay muchos precedentes en el an�lisis de la media racional, casi todos dirigidos exclusivamente al caso especial de la Mediant. Algunas de las personas que trabajaron con esa operaci�n: Nicolas Chuquet (1484), Haros(1802), Farey(1816), Cauchy, J. Wallis, C. S. Peirce, Stern-Brocot(1858-1860), D. Hidalgo (1963). Lester R. Ford y Pick.

�La media racional es la m�s elemental operaci�n aritm�tica para la resoluci�n de ra�ces y tambi�n regula las expansiones en series de potencias y la generaci�n de los n�meros transcendentales.

�La Media Aritm�nica es un caso particular de la media racional esencial en la resoluci�n de ra�ces y la cual, basados en todas las evidencias disponibles- parece haber pasado inadvertida a lo largo de toda la historia.

�Basado en todas las observaciones y m�todos descritos, resulta entonces una pat�tica arrogancia el pensar que  cualquier producto (n�meros imaginarios, sistema cartesiano, teor�a especial de la relatividad, cuarta dimensi�n, geometr�as no-euclideanas, etc.) proveniente de la opiniones y juicios personales de cualquier matem�tico pueda alguna vez superar el orden natural y las hermosas propiedades determinadas "de acuerdo al n�mero por la mente de �l qui�n cre�  todas las cosas, porque el orden fue establecido, como un esquema preliminar,...� (texto en comillas, traducci�n personal de: Nicomachus, chap.VI,[1]).

 

[TOP PAGE]

 

Copyright �

Todos los derechos reservados bajo las convenciones internacionales de derechos de autor. Ninguna parte de estas p�ginas pueden ser reproducidas, almacenadas o transmitidas en cualquier forma o por cualquier medio sin la previa autorizaci�n del autor: D. G�mez.

 

Last revision: 2002.