Root generalized continued fraction number rational irrational newton halley algorithm new math algebra mean harmonic arithmetic polynome

�   �   � � �   �

Resoluci�n de ra�ces y la Media Racional

Algunas muy breves observaciones y ejemplos extra�das del libro:�� �LA QUINTA OPERACI�N ARITM�TICA, Revoluci�n del N�mero� ISBN: 980-07-6632-4.� Copyright �. Todos los derechos reservados. Autor: D. G�mez.

 

CONTENIDO:

Nota: En esta p�gina el acr�nimo Mr debe ser interpretado como Media Racional (Rm).

Todos los ejemplos expuestos aqu� responden a un mismo principio general� el �Proceso Racional� basado en la simple operaci�n aritm�tica �Media Racional� y han sido escogidos para mostrar brevemente el alcance de este nuevo y elemental concepto aritm�tico que estuvo al alcance de cualquiera desde tiempos ancestrales, sin embargo para nuestra sorpresa no existen precedentes sobre estos simples y eficientes m�todos aritm�ticos. El lector estar� entonces en libertad de crear una inmensa variedad de nuevas funciones de iteraci�n para la resoluci�n de ecuaciones algebraicas, sin uso del sistema Cartesiano, ni decimales, ni derivadas.

 

 

 

• La resoluci�n de raices y el Proceso Racional
• Preliminares
• El Proceso Racional (RP-1) de aproximaci�n a la ra�z c�bica de 2
• Otro Proceso Racional (RP-2), relacionado con el m�todo de Bernoulli
• Proceso Racional Acelerado ARP-2a
• Proceso Racional Process ARP-2b

• Formulaci�n trivial de los m�todos de Newton y Halley por medio del Proceso Racional
• Ra�z cuadrada de P, M�todo de Newton como simple proceso racional
• Ra�z cuadrada de P, M�todo de Halley como simple proceso racional
• Ra�z c�bica de P, M�todo de Newton como simple proceso racional
• Ra�z c�bica de P, M�todo de Halley como simple proceso racional
• Ra�z cuarta de P, M�todo de Newton como simple proceso racional
• Ra�z cuarta de P, M�todo de Halley como simple proceso racional
• Ra�z quinta de P, M�todo de Newton como simple proceso racional
• Ra�z quinta de P, M�todo de Halley como simple proceso racional
• Expresi�n general del M�todo de Halley a partir del proceso racional
• Infinito n�mero de nuevas funciones de iteraci�n mediante el proceso racional
• Conclusiones

Resoluci�n de ra�ces y el Proceso Racional

La verdadera historia acerca de la resoluci�n de ra�ces

A�n a pesar de los primeros intentos de aproximaci�n num�rica de ra�ces realizados por:

 

� Babilonios (1600 B.C.) quienes trabajaron con la ra�z cuadrada de 2 (1+ 24/60 +51/60² + 10/60³, Yale No. 7289).

 

�Los matem�ticos chinos (250 B.C.) quienes desarrollaron un m�todo no-natural de ensayo y error para resolver ra�ces basado en geometr�a (gnomons), los cuales eran demasiado dif�ciles de utilizar (por no decir imposible) para ra�ces de grado superior al segundo hasta el descubrimiento muy posterior que ellos mismos hicieron del diagrama de coeficientes binomiales mal conocido  en estos d�as como el "Tri�ngulo de Pascal".

 

�Los griegos quienes aparentemente trataron de resolver ra�ces c�bicas tambi�n mediante el uso exclusivo de geometr�a  (Heron, Menaechmus) sin dejar rastros para nosotros de ning�n algoritmo de iteraci�n ni alguna aproximaci�n num�rica a�n para la ra�z cuadrada de 2.

no existen evidencias de alg�n m�todo natural (contrario al ensayo-&-error) para resolver ra�ces superiores al segundo grado desde los  Babilonios hasta la creaci�n de los decimales y el sistema cartesiano, a�n simples aproximaciones num�ricas a la ra�z c�bica son muy dif�ciles de encontrar.

La siguiente lista muestra algunas de las personas que a lo largo de la historia trataron de encontrar procesos de ensayo-&-error o simplemente aproximaciones. (Nota: Es necesario conocer muy bien la diferencia filos�fica que existe entre
un m�todo natural y un m�todo de ensayo-&-error):

�Babylonians (1600 B.C.)

�Sulbasutras (500 B.C.)

�Chi-Chang Suan-Shu, Nine Chapters (250 B.C.)

�Archimedes (225 B.C.)

�Heron (1st. century)

�Chan Heng (130)

�Chao Chung Ching (200)

� Berlin Papyrus (2nd.century)

�Theon of Alexandria (390)

�Wang Hsiao Tung (625)

�Brahmagupta (628)

�China, Ten manuals (656)

�al-Kharkhi(1020)

�Fibonacci(1202)

�Chiu Chiu Sao, Nine Sections (1247)

�Li Yeh (1248)

�Yang Hui (1261)

�Planudes (1300)

�Chu Shih Chieh (1303)

�Rhabdas (1340)

�Narayana (1350)

�Rama (1450)

�Chuquet(1484)

�Pacioli and Roche (1500-1520)

�Tonstall (1522)

�Fine (1525)

�Stifel (1544)

�Buteo (1559)

�Clavius (1585)

�Girard (1634)

En todos esos intentos a lo largo de toda la historia podemos encontrar siempre una muy extra�a insistencia en tratar de resolver los problemas propios del N�mero mediante el uso de un sistema extr�nseco a �ste como lo es la Geometr�a dando adem�s como resultado algoritmos no naturales de ensayo-&-error. Para su sorpresa, el lector comprobar� que todos esos problemas sobre resoluci�n de ra�ces que siempre fueron interpretados y aproximados de alguna manera mediante el uso del sistema cartesiano, los decimales y los infinitesimales, pod�an haber sido formulados y desarrollados exclusivamente mediante el uso de simple Aritm�tica (Media Racional).

 

Preliminaries

Es realmente sorprendente comprender que el N�mero por s� mismo nos brinda  el m�s simple camino para aproximar ra�ces. En este sentido, la muy antigua secuencia:

analizada por Nicomachus en su �Introduction to Arithmetic� y definida como �n�meros superparticulares� brinda a la luz la siguiente propiedad:

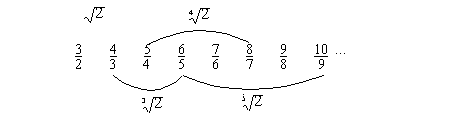
En la figura 4.1 podemos ver un conjunto de dos fracciones [3/2, 4/3] cuyo producto es trivial e igual a 2, esto es, dos aproximaciones por defecto y exceso a la ra�z cuadrada de 2.

Tambi�n otro conjunto [4/3, 5/4, 6/5] cuyo producto es trivial e igual a 2, esto es, tres aproximaciones por defecto y por exceso a la ra�z c�bica de 2.

Otro conjunto [5/4, 6/5, 7/6, 8/7] cuyo producto es trivial e igual a 2, esto es, cuatro aproximaciones por defecto y por exceso a la ra�z cuarta de 2.

Otro conjunto [6/5, 7/6, 8/7, 9/8, 10/9] cuyo producto es trivial e igual a 2, esto es, cinco aproximaciones por defecto y por exceso a la ra�z quinta de 2.

y as� sucesivamente...

Sin embargo, esta muy simple conexi�n entre esa secuencia y la resoluci�n de ra�ces pas� inadvertida para Nicomachus.

�Es que acaso los n�meros necesitan decirnos algo m�s?
Re: Por supuesto que no!
Nosotros necesitamos solamente un conjunto de n fracciones iniciales cuyo producto sea P para encontrar un proceso racional y natural basado en la Media Racional para aproximar la n-�sima ra�z de P. Podr�amos usar un n�mero infinito de conjuntos similares a los indicados por la serie de los superparticulares, pero por supuesto por ahora seleccionaremos solamente dos tipos de conjuntos que cumplen las caracter�sticas mencionadas:

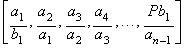
En las siguientes secciones veremos:
Algunos ejemplos num�ricos sobre algunos muy simples procesos racionales para calcular espec�ficamente la ra�z c�bica de 2, de manera que el lector podr� apreciar que los antiguos matem�ticos ten�an al alcance de la mano las herramientas aritm�ticas m�s elementales para la resoluci�n de problemas relacionados de alguna manera con lo que llamamos hoy en d�a "resoluci�n de ecuaciones algebraicas de cualquier grado".

 

Proceso racional (RP-1) de aproximaci�n a la ra�z c�bica de 2

(Nota: El acr�nimo Mr debe ser interpretado como: Media Racional (Rm)

Dado el conjunto inicial de tres valores:

cuyo producto es trivial e igual a 2. De acuerdo a nuestra notaci�n para la  media racional, el proceso racional de aproximaci�n  a la ra�z c�bica de 2 es as�:

y as� sucesivamente...

En cada paso, obtenemos un nuevo conjunto de tres aproximaciones (cuyo producto es trivial e igual a  2) por defecto y exceso a la ra�z c�bica. Es necesario resaltar que para desarrollar este proceso racional natural no hicimos uso de decimales, ni ensayo-&-error, ni sistema cartesiano, ni los infinitesimales.

Podemos expresar ese proceso racional de una manera m�s general:

Dado el conjunto inicial de tres valores:

el proceso racional hacia la ra�z c�bica de P es:

 

Otro proceso racional (RP-2), relacionado con el muy conocido m�todo de Daniel Bernoulli

Dado el conjunto inicial:

El nuevo proceso racional a la ra�z c�bica de P:

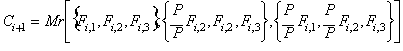
el cual converge levemente m�s r�pido que el anterior, ambos estando directamente relacionados con el conocido m�todo de Bernoulli y las fracciones continuas generalizadas.

Proceso racional acelerado ARP-2a

Dado el conjunto inicial:

Calculando las siguientes medias racionales equivalentes a la media arm�nica y aritm�tica respectivamente:

180/143 corresponde a la media arm�nica, y 227/180 a la media aritm�tica. Es f�cil encontrar un tercer valor v₃, tal que: (180/143)*(227/180)*(v₃) = 2, as�, v₃ = (2*143)/227 = 286/227. El nuevo conjunto de tres aproximaciones es:

El valor 286/227 es tambi�n una  media racional entre las tres fracciones iniciales, de manera que el proceso se transforma en un algoritmo totalmente autom�tico. Repitiendo sucesivamente los pasos anteriores y escogiendo solamente la tercera aproximaci�n de cada nuevo conjunto obtenemos la siguiente tabla que incluye una comparaci�n con los valores que se obtendr�an al usar el conocido m�todo de Newton:

Proceso Racional Acelerado  (ARP-2a)		M�todo de Newton
Aproximaciones: xi	Error	Aproximaciones: xi	Error
286  227	9E-6	63  50	8E-5
27825466  22085087	2E-12	375047  297675	-5E-9
25649277607024348370746  20357845127807416346597	7E-26	158262616209301396  125613121728942225	-2E-16

Proceso Racional ARP-2b

Dado el conjunto inicial:

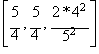
Calculando las siguientes media racionales equivalentes a las media arm�nica y aritm�tica:

Es f�cil comprobar que un tercer valor v₃, tal que: (160/127)*(63/50)*(v₃)=2, ser� v₃ = (2*127*50)/(160*63) = 635/504.

(El valor 635/504 es tambi�n una media racional entre las tres fracciones iniciales.)

Al evaluar tres pasos y tomar solamente la tercera aproximaci�n de cada nuevo conjunto, obtenemos los siguientes errores: 4 E-7, 3 E-20, 1 E-59,� 59 d�gitos exactos al valor de la ra�z en la tercera iteraci�n.

 

Desarrollo trivial de los m�todos de Newton y Halley  mediante el Proceso Racional

Ra�z cuadrada de P, el m�todo de Newton como simple proceso racional

Dado el conjunto de dos fracciones:

cuyo producto es trivial e igual a P. Haciendo sus denominadores iguales y calculando luego la media racional (Ar=Media Aritm�tica):

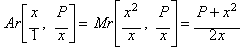
Obtenemos un valor medio entre las dos fracciones iniciales, una aproximaci�n m�s cercana al valor de la ra�z cuadrada de  P, en otras palabras, hemos obtenido una funci�n de iteraci�n equivalente al M�todo de Newton cuando es aplicado a: x²-P.

Ra�z cuadrada de P, m�todo de Halley como simple proceso racional

Dado el conjunto inicial de cuatro fracciones:

cuyo producto es trivial e igual a P², esto es, cuatro aproximaciones a la ra�z cuadrada de  P.

Calculando la  Media Aritm�nica de tercer orden (ATM₃) entre esos valores iniciales:

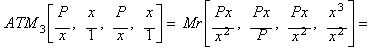
obtenemos un valor medio entre las cuatro fracciones dadas, una aproximaci�n m�s cercana al valor de la ra�z cuadrada de  P, esto es, una funci�n de iteraci�n equivalente al m�todo de Halley cuando es aplicado a la funci�n x² - P.

 

Ra�z c�bica de P, m�todo de Newton como simple proceso racional

Calculando la  media aritm�tica (Ar):

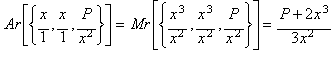
y realizando un an�lisis similar al de los casos anteriores obtenemos la funci�n de iteraci�n correspondiente al m�todo de Newton aplicado a la funci�n: x³ - P.

 

Ra�z c�bica de P, m�todo de Halley como simple proceso racional

Calculando la media aritm�nica de segundo grado (ATM₂):

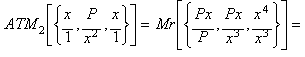
obtenemos la funci�n de iteraci�n equivalente a aplicar el m�todo de Halley a la funci�n: x³- P.

Ra�z cuarta de P, m�todo de Newton como simple proceso racional

Dado el conjunto:

de cuatro aproximaciones triviales a la ra�z cuarta de  P.

Calculando la  media aritm�tica (Ar):

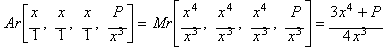
obtenemos la funci�n de iteraci�n correspondiente al m�todo de Newton aplicado a la funci�n x⁴ - P.

 

Ra�z cuarta de P, m�todo de Halley como simple proceso racional

Dado el conjunto de valores:

cuyo producto es trivial e igual a P², ocho aproximaciones a la ra�z cuarta de P.

Calculando la media aritm�nica de quinto orden ATM₅ :

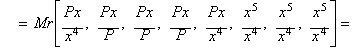
obtenemos la funci�n de iteraci�n equivalente a aplicar el m�todo de Halley a la funci�n: x⁴- P.

 

Ra�z quinta de P, m�todo de Newton como simple proceso racional

Dado el conjunto de valores:

La media aritm�tica es:

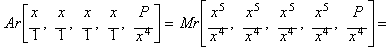
expresi�n que equivale al m�todo de Newton aplicado a la funci�n:  x⁵ - P.

 

Ra�z quinta de P, m�todo de Halley como simple proceso racional

Dado el conjunto:

La media aritm�nica de tercer orden ATM₃ da:

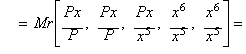
que es la funci�n de iteraci�n del m�todo de Halley aplicado a la funci�n x⁵ - P.

 

Expresi�n general del m�todo de Halley

Si continuamos con ese proceso de obtenci�n de funciones de iteraci�n para cada una de las ra�ces entonces podremos obtener la funci�n general de Halley para la ra�z de grado n de P:

 

 

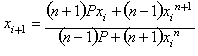
Nuevas funciones de iteraci�n

Si usted aplica la media arm�nica en lugar de la media aritm�tica en todos los casos anteriores en que era desarrollado el m�todo de Newton entonces usted obtendr� una funci�n de iteraci�n general mucho m�s eficiente que la de Newton en todo terreno. Una expresi�n general de esa funci�n para la ra�z de grado n del n�mero P ser�a :

(n* P* x)/ ((n-1)*P + x^n) .

Una vez que usted vea las ventajas de esa funci�n sobre el m�todo de Newton (requiere menos operaciones aritm�ticas, fundamentado solamente en aritm�tica) entonces entender� que basados en todas las evidencias a mano, es incre�ble que tan simples m�todos aritm�ticos no hayan aparecido en la literatura matem�tica desde los� Sumerios y Babilonios hasta nuestros d�as. Realmente incre�ble.

 

*********************************

 

Por otro lado, utilizando diferentes tipos de conjuntos iniciales es muy f�cil obtener por ejemplo una nueva funci�n de iteraci�n (IF-1) para calcular la ra�z n de  P, esa funci�n es:

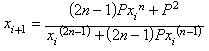
la cual triplica tambi�n el n�mero de d�gitos exactos en cada iteraci�n.

El lector podr� encontrar tambi�n otra funci�n de iteraci�n (IF-2), espec�ficamente dise�ada para la ra�z cuadrada de P:

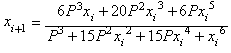
(Podr�a ser de inter�s para el lector hallar su expresi�n generalizada para calcular la ra�z n de  P )

Para el caso espec�fico de la ra�z cuadrada de 2, esa funci�n nos ofrece los siguientes valores comparados al mismo tiempo con el m�todo anterior y el de Halley:

	FI-1  Process	FI-2  Process	Halley's  Method
i	Errors
1	0.014357	-7.21 E-5	0.014214
2	3.64 E-7	-7.79 E-28	3.64 E-7
3	6.05 E-21	-1.24 E-165	6.05 E-21
4	2.77 E-62	-1.98 E-992	2.77 E-62

 

De esta manera pueden ser generados un infinito n�mero de funciones de iteraci�n.

CONCLUSIONES

Resulta realmente ins�lito que m�todos tan simples como los indicados aqu� no aparezcan mencionados en ning�n texto sobre n�meros. Basados en estos procesos aritm�ticos extremadamente simples y considerando la incompresible ausencia de precedentes en esta materia a lo largo de toda la historia matem�tica, cualquier persona puede comprender ahora que es ciertamente  una rid�cula arrogancia el pensar que las artificiales creaciones personales (ej.: sistema cartesiano, fracciones decimales, n�meros imaginarios, etc.) de cualquier individuo egoc�ntrico pudieran alguna vez sobrepasar el orden natural predeterminado por Dios en acuerdo con las armon�as del N�mero.

[TOP PAGE]

 

Copyright �

Todos los derechos reservados bajo las convenciones internacionales de derechos de autor. Ninguna parte de estas p�ginas pueden ser reproducidas, almacenadas o transmitidas en cualquier forma o por cualquier medio sin la previa autorizaci�n del autor: D. G�mez.

 

Last revision: 2002.